Four color theorem

The Four color theorem is the challenge to draw first a map consisting of different 'countries' and then to color the different countries with a minimum number of colors. The minimal number is 4.
The line between each country is called a boundary. There is one constrain involved.

1. The constrain is that the maximum number of countries involved at each point on the boundary is three. This meant there can be no point where 4 countries meet.

For more detail select: https://en.wikipedia.org/wiki/Four_color_theorem For the source of the program select: Four_color_theorem.xls.zip
This zip file consists of two copies of the program:

1. Four_color_theorem.xls This program is the real program and contains 10 simulations.
2. Four_color_theorem_test.xls This is the same as above, but is more meant to try your own examples.

There is also a painting by the author, which demonstrates the 4 color Theorem. To see the painting select: 4 Color theorem
For further reading select: http://www.ams.org/notices/200811/tx081101382p.pdf "Formal Proof—The Four Color Theorem" by Georges Gonthier

Page description and operation

Each Page or Blad consits of 3 parts: A left part, a center part and a right part.

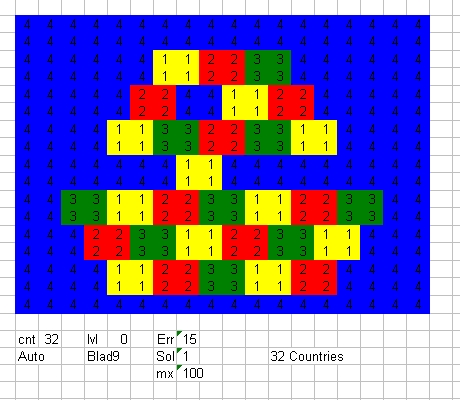
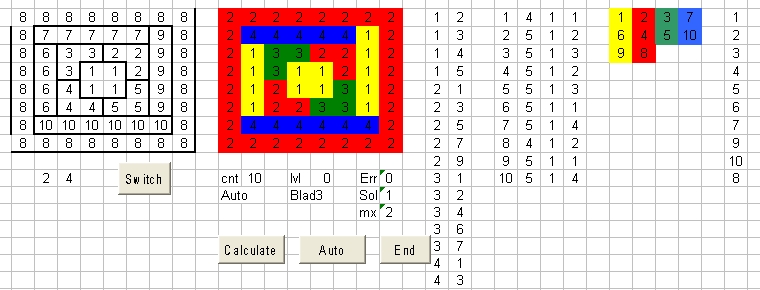
• The Left part contains the Target Map and one Command Button: Switch.
• The Center part contains 4 command buttons: Calculate , Mode End and Wait.
  The Center part also contains five program parameters, discussed below.
• The Right part is divided in 4 sections and contains the intermediate results of the program. For more info see below.

Picture 1

• The Left Map is called the Target Map and shows the layout of all the countries used. Each country is identified with a number. The primary purpose is to define each country and draw the borders of each country.
• The Center Map is called the Result Map and also shows the layout all the countries but now each with its own calculated color.
• The Calculate button is used to perform a simulation and to calculate, based on the Target Map drawn, the actual colors in the Result Map.
  Before the Calculate button it is important to select the Mode button.
• The Mode button has four values or modes: "Continuous", "Auto", "Manual" and "Step".
  
  • The normal mode is the "Auto" mode. When the "Auto" mode is selected and the Calculate button is selected the simulation will start and slowly each country will given a color.
    when the complete map is colored the calculation will show the End button and the Wait button button. This defines one solution.
    However the simulation is not finished
    You have now two options. They are important.
    • When the the End button is selected the program will terminate. When finshed the program will show the Calculate and "Auto" Mode button.
    • When the Wait command button is selected a next solution will be calculated.
    The central program in the simulation is called Maximum2. This is a recursive program which calls itself. When this program calls itself the parameter level is increased. When the program is finised the parameter level is decreased.
    When the "Manual" Mode mode is selected each time when the level parameter is increased the calculation will go into the "Wait" state.
    
  • The Step mode is the most accurate mode to investigate what the calculation does. After each step the calculation
  • There is also an extra mode called the Continues mode. When this mode is selected the calculation will go through all the possible solutions, without stopping.
• The End mode button is used to terminate the simulation. The End command button is direct displayed after the Calculation command is selected and is normally used in combination with the "Auto", "Manual" and "Step" Mode button in combination with the Wait button.
  The End mode button can also be used in combination with the "Continuous" Mode button to terminate this simulation. To stop such a simulation is not easy. The End mode button has to be used at least twice. The first time the 5 parameter display area will display STOP. The second time the simulation will terminate.
• The Switch mode is only important for the target map. The command is used to change two country numbers. Near the Switch button two parameters are displayed.
  When these two parameters are for example 2 and 4 and the Switch command is selected then each cell which contains a 2 is changed in a 4 and vice versa. When the Switch command is selected again (no parameter change) the original situation is restored.
  Changing county numbers can have influence about the actual solution calculated.

Parameters of the program

The program uses 5 parameters: cnt, lvl, Err, Sol and Max

• The parameter cnt shows the number of countries colored in progress. The final number should be the same as the number of countries.
• The parameter lvl shows the number of levels in the recursive subroutine Maximum2. See below in the section: Excel Program description
• The parameter Err shows the number of errors detected. Normally this means that there currently is no solution. Normally this means that the subroutine Maximum2 terminates, countries are cleared and continues at a lower level.
• The parameter Sol shows the number of solutions counted. In the "Auto" mode this value is 1 when the program finds a solution. In the "Continues" mode this value slowly increases.
• The parameter Max defines the maximum number of solutions accepted. This value is only used in the "Continues" mode. When the The parameter Sol reaches the parameter Max value, the program stops.

The 5 parameter display area also contains 3 additional parameters:

• A Copy of mode of the Mode command button.
• The parameter name. This is name of the active "Blad". Normally the parameter name is the name of the selected "Blad".
  When Blad7 is selected the parameter name shows Blad7. This is also the case when Calculation button is selected. However when during this calculation a different "Blad" is selected, for example Blad8 then parameter name of Blad8 will show Blad7 and not Blad8, because the calculation started with Blad7 is not finished.
• The parameter STOP after the End button is selected during a running simulation

The right side of the display.

The right side shows the results of each simulation and is subdivided in 4 sections.
Section 1 consists of 2 columns. Section 2 of 4. Section 3 of 4 and Section 4 of 1.

• Section 1 shows the country numbers which surround each country.
  When there are n countries Column 1 shows the numbers from 1 to n.
  Column 2 shows first the country numbers which surround country 1. Next the country numbers which surround #2 etc until country n.
  Section 1 shows an important rule. If one country is surrounded by three countries they should have the color numbers 1,2,3 and 4.
• Section 2 shows the most important information as the simulation progresses.
  Column 1 shows the country # from 1 to 4. Column 2 shows the number of countries that surround a specific country. Column 3 shows the number of colors that are availble for a specific country. Initial this value is 4.
  When for a certain country a specific color is selected this value changes to 1 and the total number of available colors for the surrounded countries is decreased by one. Column 4 contains the final color number.
• Section 3 shows the final country numbers for each country.
  Column 1 shows the country number for color 1 i.e. yellow. Column 2 shows the country number for color 2 i.e. red. Column 3 shows the country number for color 3 i.e. green. Column 4 shows the country number for color 4 i.e. blue.
• Section 4 shows the final order of the countries as filled in.

Program Four_color_theorem.xls

The Program Four_color_theorem.xls contains 10 simulations.
The first time user is adviced to select each simulation in succession and not to perform any calculation. Generally speaking the higher examples are the most difficult.
When you observe the results you will see that below each result a field marked "Err". The number behind that field identifies the number of errors detected.
In Blad1 the values is 0. In Blad2: 0. In Blad3: 0. In Blad4 0: In Blad5: 0. In Blad6: 0. In Blad7: 1. In Blad8: 8 and in Blad9: 14.
When you study Blad7, Blad8 and Blad9 you can easily see that there is an increase in complexity.

When you are finished you can select the "calculate" button for each simulation. Keep the mode "Auto". When the simulation is finished select the End Command button. Specific observe the lvl parameter and the END of each simulation.
In Blad1 the value lvl parameter is 1. In Blad2: 1. In Blad3: 2. In Blad4 3: In Blad5: 6. In Blad6: 6. In Blad7: 4. In Blad8: 4 and in Blad9: 14.

What follows is a short description of each simulation or "Blad"

1. "Blad1" is very easy. The parameter lvl is 1 and # of errors 0
2. "Blad2" is also easy. The parameter lvl is 1 and # of errors 0
3. "Blad3" is shown in Picture 1. The parameter lvl is 2 and # of errors 0
4. "Blad4" the parameter lvl is 3 and # of errors 0
5. "Blad5" demonstrates the top part of the "4 Color theorem" painting. The tail and legs are not included. The simulation shows 36 countries.
   The parameter lvl is 6 and # of errors 0
6. "Blad6" demonstrates the bottom part of the "4 Color theorem" painting. The tail and legs are not included. The simulation shows 37 countries.
   The difference between "Blad5" and "Blad6" is in country number 17, which is divided in two (Country #17 and country #37). This only difference has a large influence. The more or less 15 countries in the center are the same. The other countries have different colors. The parameter lvl is 6 and # of errors 0
7. "Blad7" Shows a rather simple example. In the center there is one green country with the number 3. It is possible to make this country blue with the number 4. That means the inner part of 12 countries has only the numbers 1,2 and 4. It is easy to see that you can copy this country and make the inner part twice as large, only with three colors. etc etc.
8. "Blad8" is the same as "Blad7" with only one country added.
   The parameter lvl is 4 and # of errors 5
9. "Blad9" is the same as "Blad8" with more or less the inner part of "Blad7" copied.
   The parameter lvl is 11 and # of errors 15
   See also "Blad9" of paragraph Four_color_theorem_test.xls
   
10. "Blad10" is the same as "Blad9" with only one country missing. See also paragraph Four_color_theorem.xls Blad9 and Blad 10 .

Program Four_color_theorem_test.xls

The program Four_color_theorem_test.xls also contains 10 simulations.
In the program Four_color_theorem.xls each simulation always shows two maps: The "Target map" and the "Result map".
The Four_color_theorem_test.xls program sometimes contains a third map called the "User map".
The "User map" is a copy of the original "Target map" as original build, including some errors.
When you want to perform any simulation which also contains a "User map" you should first check that the "Target map" is the same as the "User map". When that is not the case you should copy the "User map" onto the "Target map".
To get an impression about each simulate use the "Auto" mode.

What follows is a short description of each simulation or "Blad"

1. "Blad1" contains a "User map" and is used to demonstrate a situation where four countries meet each other at one point. There are two of these situations. The demonstration also shows a third situation where four countries meet, when two countries have the same number.
   The user should perform a simulation (Select Calulate) and observe the three errors. Next to make the necessary modifications in the "Target map" and try again.
2. "Blad2" is used to demonstrate the simulation discussed in https://en.wikipedia.org/wiki/Four_color_theorem#False_disproofs
3. "Blad3"
4. "Blad4" is used what happens if not all the countries are created. For example country #1 is missing.
5. "Blad5" Is used to simulate that it is only required to indicate the outer corners of each simulation. Most of the empty numbers are filled in automatically. b>"Blad5" is also used to demonstrate 1 small error. It is difficult to find by visual inspection. Try it.
   Otherwise select "calculate".
6. "Blad6"
7. "Blad7"
8. "Blad8"
9. "Blad9"
10. "Blad10" Shows an example of the 50 states of the USA. 2 states are not shown. The parameter lvl is 13 and # of errors 2
    

Four_color_theorem.xls Blad9 and Blad 10

When you don't select Picture 2 the image shows 32 countries of Blad9 of the program Four_color_theorem.xls. The number of levels is 11 and the number of errors is 15 that means it is an easy configuration.
The purpose of this particular example is to demonstrate what happens if one country is deleted.
You will see that when you select picture 2.

Picture 2

When picture 2 is selected the image shows 31 countries of Blad10 of the program Four_color_theorem.xls. The number of errors has increased to 41835. The only difference is in country #25 of Blad9. This country is missing in Blad10. This only one difference is quite amazing because to perform the simulation takes very long.
The main reason for this change in performance is country #9. The color has to be red. Country #9 is the country right above the yellow country in the center.
When you look carefull you can also see that there is a solution with only the outer border (Country #15) is blue.

Excel Program description

The excel program more or less consists of two parts.

• The first part is used to create a map of of countries. The Excel program Four_color_theorem_test.xls is used to demonstrate that functionality.
• The second part is used to color the countries of each map.

Main Initialize Init Store Macro_Right Macro_Bottom CrossTest Optimize_mat Optimize_mat1 Replace Optimize_game Tgame Calculate1 Maximum1 Wait Maximum2 Process Test_kleur Test_kleur2 Clearmap Exit sub ' one choice Test_Mat_kleur Map_kleur Exit sub ' two choices Do Test_mat Test_Mat_kleur Map_kleur Error --> Exit Maximum2 Loop Maximum3 Test_mat Test_Mat_kleur Map_kleur Maximum2 Wait

The three most important subroutines are Maximum1, Maximum2 and Maximum3. Subroutine Maximum1 calculates the first three countries. Subroutine Maximum2 is a recursive subroutine. This subroutine first calls the subroutine Process. Next it selects countries based on two criteria: When there is only one choice the country is selected and Maximum2 terminates When there are two choices we have what is called a fork. One country is selected and the subroutine Maximum2 is called again. When these criteria are not enough it calls the sub Maximum3. Subroutine Maximum3 is called to make a more complex choice between which country has to be selected. Subroutine Process selects colors using the subroutines Test_kleur and Test_kleur2 Subroutine Test_kleur tests if only one color is possible. The subroutine tests of each country the colors of each surrounding country. When the number of colors of the surrounding countries is three then the color of the tested country is #4. Subroutine Test_kleur2 tests if only one color is possible. The subroutine tests of each country the colors of each surrounding country and the number of countries that have no color. When the number of colors of the surrounding countries is two and the number of free countries is 0 or 1 then color of the tested country can be anyone of the two not used colors.

Reflection part 1 - prove

The first purpose of the simulation is to demonstrate that it is possible to color each combination of countries under the rule that nowhere there should be any point where 4 countries meet.
The second purpose is to prove that this is possible. The point is that you can never test each and every combination. In reality only a limited one. The question which minimal set of countries is sufficient as a prove that the 4 color theorem is valid for all combinations.

You can also use the same concept as raised by the following question: How do you prove that a perpetual motion machine does not work? Built one.
Until now all the simulations that did not work are caused by programming errors.
At 15 december 2018 a programming conceptual error was discovered in the subroutine process. The subroutine first calls Test_kleur and secondly Test_kleur2
In principle after making this second call the first subroutine should be called again. Now the two are called in a loop until no change is detected.
At 15 december 2018 also a programming error was detected in subroutine test_kleur2. The structure setup was not correct for the last country tested. The structure was changed.

Reflection part 2

Feedback

Back to my home page Contents of This Document